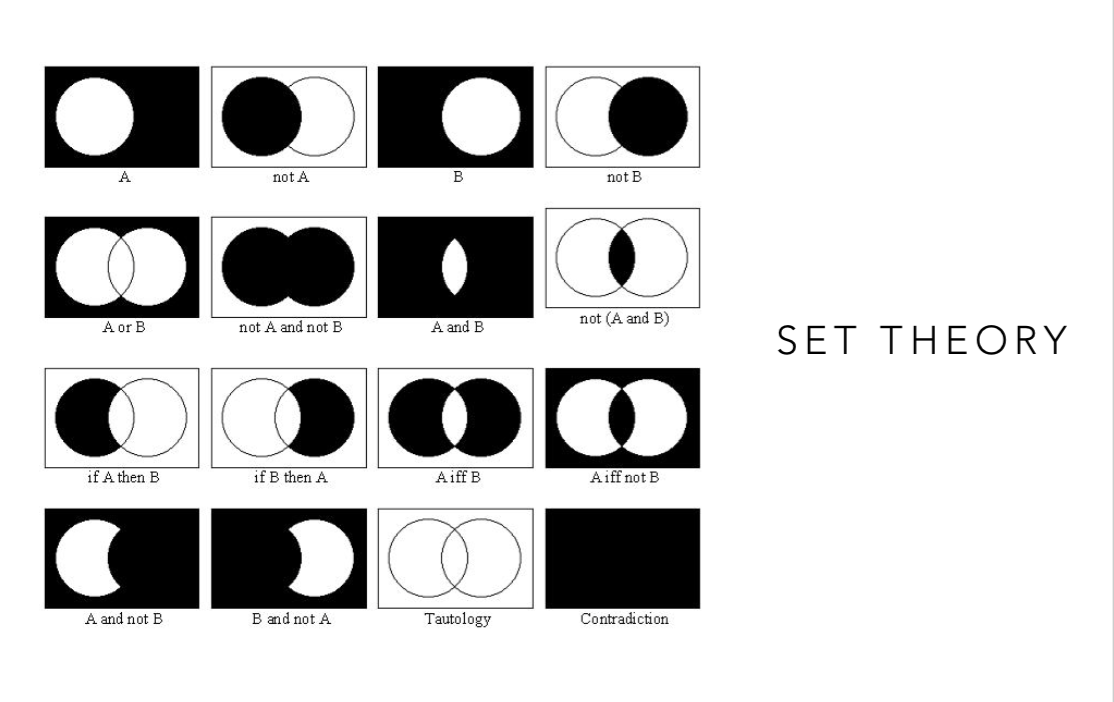
Set Theory is a branch of mathematics that studies sets or the collection of objects. In relation to Big Data, the cataloging and the creating of collections of information is where this project begins. Viewing the world as a massive network, everything can be viewed a data point, but also, when collected, becomes part of a set. And what defines any data point is the metadata that defines it and links it to that set of data.
'<'META'>' Methods attempts to extract beauty and information from the superset of information. This projects looks not at the individual (micro) but at the whole (macro) and attempts to find relationships, whether contextual, graphical or mathematical, by examining metadata.
This project also reimagines digital curation and asks the question: can a collection of digital assets become an asset, or work of art, in and of itself? Is metadata the “paint” that we can mix together, through algorithmic search, to create new “colors” in our digital “canvas”?
By applying mathematical theory to the analysis of a digital collection (set) of objects what new relationships can be uncovered and what new art can evolve?